실수의 형태는 float, double으로 2가지 형태가 있는데
float는 4byte
double는 8byte를 갖는다
그렇지만 int형 도 4byte인데 float과 int형이 같은 메모리 크기를 갖는건 무언가 이상하다.
그이유인 지수와 가수에 대하여 알아보자
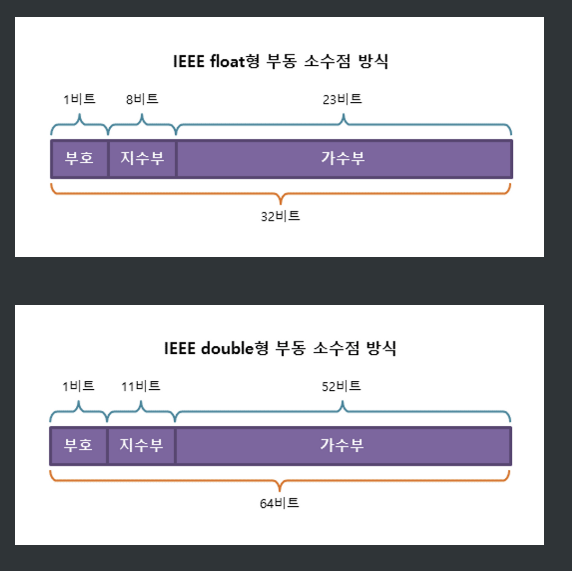
상단의 사진은 IEEE가 제공하는 부동소수점 방식의 형태인데 가수부와 지수부의 크기가 다른것을확인할수 있다
이러한 이유는
float형은 4byte -> 32bit이며 (7자리)
double형은 8byte -> 64bit를 (15자리)갖는데 이것은 표현하는 자릿수의 차이이며
이를 설명하기 위한 코드는 아래와같다
//코드1
int a = 1;
float b = 1.1f; (float은 뒤에 f붙이기)
double c = 1.1;
//자리수 테스트
float testFloat = 0.1234567890123456789f;
double testDouble = 0.1234567890123456789;
System.out.println(testFloat);
System.out.println(testDouble);
코드1과 사진1을 참조하면 뒤의 자릿수가 2배차이나는것 확인할수 있고 뒤의 숫자는 자릿수를 넘어간 관계로 자동적으로 반올림 된것을 확인할수 있다.
조금더 자세하게 설며하면 하단의 사진을 참조하면 된다.

부동 소수점 방식은 부호는+(0) 또는 1(-)으로 제일 앞쪽에 , 지수, 가수로 나뉘는데
가수 - 곱하는수 (2)
지수 - 제곱하는 부분을 뜻하며
float은 128~126 (256 = 2^8)으로 총 구현 가능한 숫자는 128+126+0 총 255 이며 여기에 bias(127)을 추가하여 총 256이 나오는것이다.
1024,-1022(총 구현가능한 숫자는 1024+1022+0으로 총 2047개이며 1024 = 2^10) 여기서도 bias(1023)을 추가하여 2048이 되는것이다.
여기서 의문을 가질것은 지수부분과 가수부분의 비트가 23,52로 측정된 이유가 궁금할것이다.
이것은 소수점 표현방식의 차이로 나타나는 숫자이다.
실수의 표현방식은 고정소수점, 부동소수점 방식이 있는데 float형을 기준으로 설명하자면 아래와 같다.
고정소수점
float의 경우 32bit를 부호 (1bit), 정수(15bit),소수(16bit)로 구분하는 방식인데 이는 정밀한 값을 표현할수 없다는 단점이 있다 (정수가 20bit로 넘어가거나 소수가 20bit로 넘어가는 경우 정확한 값이 출력할수 없다.)
부동소수점
고정소수점의 정확한 값을 표현하지 못한다는 문제점을 보완한 방식으로 모든 2진수 숫자를 1.xxx의 형태로 출력하는 것으로 현재 가장 보편적으로 사용된다.
32bit를 부호(1bit), 소수점이 움직일 위치 - 지수부(8bit), 소수점이 움직인 결과에서 소수점 뒤로 오는 부분을 채워넣는것(23bit)
double형의 경우 지수부에 11bit를 할당해 더 많은 양(소수점이 움직일수 있는 범위가 커짐)을 저장할수 있게된것이다.

bias
IEEE에선 지수에 해당하는 숫자 + bias(127)을 더한 숫자가 2진수로 바뀌어 들어가는데
bias를 쓰는 이유는 지수가 음수일수도 있기 때문에 들어가는것이다.
float의 경우 -126~128인데 두 숫자의 중간값인 127을 할당했고
double의 경우 - -1022~1024인데 두 숫자의 중간값이 1023을 할당한것이다.
'JAVA' 카테고리의 다른 글
| 클래스 변수,인스턴스 변수 (1) | 2023.01.30 |
|---|---|
| 인터페이스란? (3) | 2023.01.13 |
| JPA란 무엇인가 (0) | 2022.12.23 |
| 3항 연산자에 관하여 (2) | 2022.12.22 |
| 라이브러리와 프레임워크 (1) | 2022.12.20 |